In 1999, while sitting at a bus stop in Cuernavaca, Mexico, a Czech physicist named Petr Šeba noticed young men handing slips of paper to the bus drivers in exchange for cash. It wasn’t organized crime, he learned, but another shadow trade: Each driver paid a “spy” to record when the bus ahead of his had departed the stop. If it had left recently, he would slow down, letting passengers accumulate at the next stop. If it had departed long ago, he sped up to keep other buses from passing him. This system maximized profits for the drivers. And it gave Šeba an idea.
“We felt here some kind of similarity with quantum chaotic systems,” explained Šeba’s co-author, Milan Krbálek, in an email.
After several failed attempts to talk to the spies himself, Šeba asked his student to explain to them that he wasn’t a tax collector, or a criminal — he was simply a “crazy” scientist willing to trade tequila for their data. The men handed over their used papers. When the researchers plotted thousands of bus departure times on a computer, their suspicions were confirmed: The interaction between drivers caused the spacing between departures to exhibit a distinctive pattern previously observed in quantum physics experiments.
“I was thinking that something like this could come out, but I was really surprised that it comes exactly,” Šeba said.
Subatomic particles have little to do with decentralized bus systems. But in the years since the odd coupling was discovered, the same pattern has turned up in other unrelated settings. Scientists now believe the widespread phenomenon, known as “universality,” stems from an underlying connection to mathematics, and it is helping them to model complex systems from the Internet to Earth’s climate.
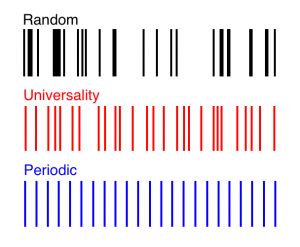
Illustration by Simons Science News
The red pattern exhibits a precise balance of randomness and regularity known as “universality,” which has been observed in the spectra of many complex, correlated systems. In this spectrum, a mathematical formula called the “correlation function” gives the exact probability of finding two lines spaced a given distance apart.
The pattern was first discovered in nature in the 1950s in the energy spectrum of the uranium nucleus, a behemoth with hundreds of moving parts that quivers and stretches in infinitely many ways, producing an endless sequence of energy levels. In 1972, the number theorist Hugh Montgomery observed it in the zeros of the Riemann zeta function, a mathematical object closely related to the distribution of prime numbers. In 2000, Krbálek and Šeba reported it in the Cuernavaca bus system. And in recent years it has shown up in spectral measurements of composite materials, such as sea ice and human bones, and in signal dynamics of the Erdös–Rényi model, a simplified version of the Internet named for Paul Erdös and Alfréd Rényi.
Each of these systems has a spectrum — a sequence like a bar code representing data such as energy levels, zeta zeros, bus departure times or signal speeds. In all the spectra, the same distinctive pattern appears: The data seem haphazardly distributed, and yet neighboring lines repel one another, lending a degree of regularity to their spacing. This fine balance between chaos and order, which is defined by a precise formula, also appears in a purely mathematical setting: It defines the spacing between the eigenvalues, or solutions, of a vast matrix filled with random numbers.
“Why so many physical systems behave like random matrices is still a mystery,” said Horng-Tzer Yau, a mathematician at Harvard University. “But in the past three years, we have made a very important step in our understanding.”
By investigating the “universality” phenomenon in random matrices, researchers have developed a better sense of why it arises elsewhere — and how it can be used. In a flurry of recent papers, Yau and other mathematicians have characterized many new types of random matrices, which can conform to a variety of numerical distributions and symmetry rules. For example, the numbers filling a matrix’s rows and columns might be chosen from a bell curve of possible values, or they might simply be 1s and –1s. The top right and bottom left halves of the matrix might be mirror images of one another, or not. Time and again, regardless of their specific characteristics, the random matrices are found to exhibit that same chaotic yet regular pattern in the distribution of their eigenvalues. That’s why mathematicians call the phenomenon “universality.”
“It seems to be a law of nature,” said Van Vu, a mathematician at Yale University who, with Terence Tao of the University of California, Los Angeles, has proven universality for a broad class of random matrices.
Universality is thought to arise when a system is very complex, consisting of many parts that strongly interact with each other to generate a spectrum. The pattern emerges in the spectrum of a random matrix, for example, because the matrix elements all enter into the calculation of that spectrum. But random matrices are merely “toy systems” that are of interest because they can be rigorously studied, while also being rich enough to model real-world systems, Vu said. Universality is much more widespread. Wigner’s hypothesis (named after Eugene Wigner, the physicist who discovered universality in atomic spectra) asserts that all complex, correlated systems exhibit universality, from a crystal lattice to the Internet.
The more complex a system is, the more robust its universality should be, said László Erdös of the University of Munich, one of Yau’s collaborators. “This is because we believe that universality is the typical behavior.”
In many simple systems, individual components can assert too great an influence on the outcome of the system, changing the spectral pattern. With larger systems, no single component dominates. “It’s like if you have a room with a lot of people and they decide to do something, the personality of one person isn’t that important,” Vu said.
Illustration by Matt Britt
Mathematicians are using random matrix models to study and predict some of the Internet’s properties, such as the size of typical computer clusters.
Whenever a system exhibits universality, the behavior acts as a signature certifying that the system is complex and correlated enough to be treated like a random matrix. “This means you can use a random matrix to model it,” Vu said. “You can compute other parameters of the matrix model and use them to predict that the system may behave like the parameters you computed.”
This technique is enabling scientists to understand the structure and evolution of the Internet. Certain properties of this vast computer network, such as the typical size of a cluster of computers, can be closely estimated by measurable properties of the corresponding random matrix. “People are very interested in clusters and their locations, partially motivated by practical purposes such as advertising,” Vu said.
A similar technique may lead to improvements in climate change models. Scientists have found that the presence of universality in features similar to the energy spectrum of a material indicates that its components are highly connected, and that it will therefore conduct fluids, electricity or heat. Conversely, the absence of universality may show that a material is sparse and acts as an insulator. In new work presented in January at the Joint Mathematics Meetings in San Diego, Calif., Ken Golden, a mathematician at the University of Utah, and his student, Ben Murphy, used this distinction to predict heat transfer and fluid flow in sea ice, both at the microscopic level and through patchworks of Arctic melt ponds spanning thousands of kilometers.
The spectral measure of a mosaic of melt ponds, taken from a helicopter, or a similar measurement taken of a sample of sea ice in an ice core, instantly exposes the state of either system. “Fluid flow through sea ice governs or mediates very important processes that you need to understand in order to understand the climate system,” Golden said. “The transitions in the eigenvalue statistics presents a brand new, mathematically rigorous approach to incorporating sea ice into climate models.”
The same trick may also eventually provide an easy test for osteoporosis. Golden, Murphy and their colleagues have found that the spectrum of a dense, healthy bone exhibits universality, while that of a porous, osteoporotic bone does not.

Don Perovich
When Arctic melt ponds are sufficiently connected, as pictured here, they exhibit a property called universality that researchers believe is common to all complex, correlated systems.
“We’re dealing with systems where the ‘particles’ can be on the millimeter or even on the kilometer scale,” Murphy said, referring to the systems’ component parts. “It’s amazing that the same underlying mathematics describes both.”
The reason a real-world system would exhibit the same spectral behavior as a random matrix may be easiest to understand in the case of the nucleus of a heavy atom. All quantum systems, including atoms, are governed by the rules of mathematics, and specifically by those of matrices. “That’s what quantum mechanics is all about,” said Freeman Dyson, a retired mathematical physicist who helped develop random matrix theory in the 1960s and 1970s while at Princeton’s Institute for Advanced Study. “Every quantum system is governed by a matrix representing the total energy of the system, and the eigenvalues of the matrix are the energy levels of the quantum system.”
The matrices behind simple atoms, such as hydrogen or helium, can be worked out exactly, yielding eigenvalues that correspond with stunning precision to the measured energy levels of the atoms. But the matrices corresponding to more complex quantum systems, such as a uranium nucleus, quickly grow too thorny to grasp. According to Dyson, this is why such nuclei can be compared to random matrices. Many of the interactions inside uranium — the elements of its unknown matrix — are so complex that they become washed out, like a mélange of sounds blending into noise. Consequently, the unknown matrix that governs the nucleus behaves like a matrix filled with random numbers, and so its spectrum exhibits universality.

Don Perovich
These disconnected Arctic melt ponds do not form a system that is correlated enough to exhibit universality. Instead, the energy spectrum of the system is random.
Scientists have yet to develop an intuitive understanding of why this particular random-yet-regular pattern, and not some other pattern, emerges for complex systems. “We only know it from calculations,” Vu said. Another mystery is what it has to do with the Riemann zeta function, whose spectrum of zeros exhibits universality. The zeros of the zeta function are closely tied to the distribution of the prime numbers — the irreducible integers out of which all others are constructed. Mathematicians have long wondered at the haphazard way in which the primes are sprinkled along the number line from one to infinity, and universality offers a clue. Some think there may be a matrix underlying the Riemann zeta function that is complex and correlated enough to exhibit universality. Discovering such a matrix would have “big implications” for finally understanding the distribution of the primes, said Paul Bourgade, a mathematician at Harvard.
Or perhaps the explanation lies deeper still. “It may happen that it is not a matrix that lies at the core of both Wigner’s universality and the zeta function, but some other, yet undiscovered, mathematical structure,” Erdös said. “Wigner matrices and zeta functions may then just be different representations of this structure.”
Many mathematicians are searching for the answer, with no guarantee that there is one. “Nobody imagined that the buses in Cuernavaca would turn out to be an example of this. Nobody imagined that the zeroes of the zeta function would be another example,” Dyson said. “The beauty of science is it’s completely unpredictable, and so everything useful comes out of surprises.”
